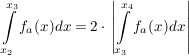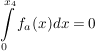Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
Sigrid Sprock
Marc O. Sandlus | www.matheraum.de
Vorbereitung auf das Zentralabitur in Mathematik in NRW
Aufgabenblatt 1
Abgabe: Fr 10.07.2009 16:00 | 22.09.2006 | | Aufgabe 1 | Flächenstrategien
Gegeben sind die Funktionen 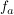 mit mit 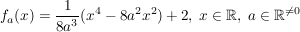 . .
a) Untersuchen Sie für a > 0 den Graphen zu 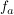 auf Symmetrie sowie auf sein Verhalten für auf Symmetrie sowie auf sein Verhalten für 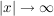 . Bestimmen Sie die Extrem- und Wendepunkte des Graphen in Abhängigkeit von a. . Bestimmen Sie die Extrem- und Wendepunkte des Graphen in Abhängigkeit von a.
b)
1. Bestimmen Sie denjenigen Wert von a, für den der zu 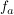 gehörende Graph einen Extrempunkt auf der x-Achse hat. gehörende Graph einen Extrempunkt auf der x-Achse hat.
2. Beschreiben Sie den Verlauf der Graphen für negative Werte a und begründen Sie Ihre Aussage.
3. Bestimmen Sie die Anzahl der Nullstellen von f in Abhängigkeit von a.
4. Ermitteln Sie alle Werte für a, so dass der Graph zu 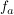 durch den Punkt P( 2 | 0 ) verläuft. durch den Punkt P( 2 | 0 ) verläuft.
5. Alle Graphen in der Zeichnung unten gehören zur Schar 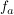 . Geben Sie jeweils das passende a an bzw. den Bereich, aus dem der zugehörige Wert von a stammt, und begründen Sie Ihre Zuordnung. . Geben Sie jeweils das passende a an bzw. den Bereich, aus dem der zugehörige Wert von a stammt, und begründen Sie Ihre Zuordnung.
![[Dateianhang]](uploads/forum/00180373/forum-i00180373-n001.png)
c) Es soll die folgende Problemstellung bearbeitet werden:
"Bestimmen Sie den Wert von a (a > 1), für den der Inhalt der vom Graphen zu 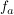 und der x-Achse oberhalb der x-Achse eingeschlossenen Fläche gleich dem Inhalt der Flächen ist, die die x-Achse und der Graph unterhalb der x-Achse umschließen." und der x-Achse oberhalb der x-Achse eingeschlossenen Fläche gleich dem Inhalt der Flächen ist, die die x-Achse und der Graph unterhalb der x-Achse umschließen."
Zur Lösung werden die Vorschläge V 1 und V 2 gemacht:
V1: Ich bestimme die Nullstellen  mit mit 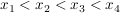 und löse die Gleichung und löse die Gleichung
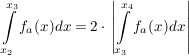 . .
V2: Ich bestimme die Nullstellen  mit mit 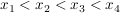 und löse die Gleichung und löse die Gleichung
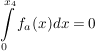 . .
Beurteilen Sie diese beiden Vorschläge. |
Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
|

![[Dateianhang]](uploads/forum/00180373/forum-i00180373-n001.png)